2.9 The Formal Definition of a Limit
A “rigorous proof” in mathematics is a proof based on a complete chain of logic without any gaps or ambiguity. The formal limit definition is a key ingredient of rigorous proofs in calculus. A few such proofs are included in Appendix D. More complete developments can be found in textbooks on the branch of mathematics called “analysis.”
In this section, we reexamine the definition of a limit in order to state it in a more rigorous and precise fashion. Why is this necessary? In Section 2.6, we defined limits by saying that \(\lim\limits_{x\rightarrow c}f(x)=L\) if \(|f(x)-L|\) becomes arbitrarily small when \(x\) is sufficiently close (but not equal) to \(c\). The problem with this definition lies in the phrases “arbitrarily small” and “sufficiently close.” We must find a way to specify just how close is sufficiently close.
This paragraph is just for keeping Read On button from covering margin note. Hidden at publish.
This paragraph is just for keeping Read On button from covering margin note. Hidden at publish.
This paragraph is just for keeping Read On button from covering margin note. Hidden at publish.
This paragraph is just for keeping Read On button from covering margin note. Hidden at publish.
2.9.1 The Size of the Gap
Recall that the distance from \(f(x)\) to \(L\) is \(| f(x) - L |\). It is convenient to refer to the quantity \(|f(x)-L|\) as the gap between the value \(f(x)\) and the limit \(L\).
Let’s reexamine the trigonometric limit
\[\lim\limits_{x\rightarrow 0}\frac{\sin x}{x} = 1 \tag{1}\]
In this example, \(f(x)=\tfrac{\sin x}{x}\) and \(L = 1\), so Eq. (1) tells us that the gap \(|f(x) - 1|\) gets arbitrarily small when \(x\) is sufficiently close, but not equal, to \(0\) [Figure 2.48(A)].
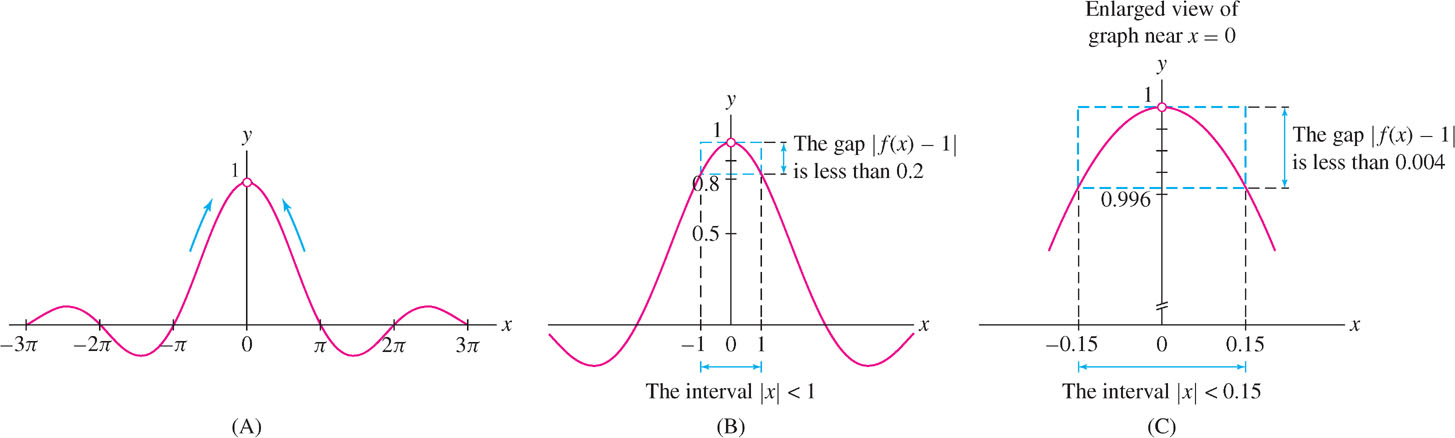
Suppose we want the gap \(|f(x) - 1|\) to be less than \(0.2\). How close to \(0\) must \(x\) be? Figure 2.48(B) shows that \(f(x)\) lies within \(0.2\) of \(L = 1\) for all values of \(x\) in the interval \([-1, 1]\). In other words, the following statement is true:
\[\left|\frac{\sin x}{x} - 1\right| < 0.2 \text{ if }0<|x|<1\]
111
If we insist instead that the gap be smaller than \(0.004\), we can check by zooming in on the graph, as in Figure 2.48(C), that
\[\left|\frac{\sin x}{x} - 1\right| < 0.004 \text{ if }0<|x|<0.15\]
It would seem that this process can be continued: By zooming in on the graph, we can find a small interval around \(c = 0\) where the gap \(|f(x) - 1|\) is smaller than any prescribed positive number.
To express this in a precise fashion, we follow time-honored tradition in using the Greek letters \(\epsilon\) (epsilon) and \(\delta\) (delta) to denote small numbers specifying the sizes of the gap and the quantity \(|x - c|\), respectively. In our case, \(c = 0\) and \(|x - c| = |x|\). The precise meaning of Eq. (1) is that for every choice of \(\epsilon > 0\), there exists some \(\delta\) (depending on \(\epsilon\)) such that
\[\left|\frac{\sin x}{x} - 1\right| < \epsilon \text{ if }0<|x|<\delta\]
The number \(\delta\) pins down just how close is “sufficiently close” for a given \(\epsilon\). With this motivation, we are ready to state the formal definition of the limit.
The formal definition of a limit is often called the \(\epsilon-\delta\) definition. The tradition of using the symbols \(\epsilon\) and \(\delta\) originated in the writings of Augustin-Louis Cauchy on calculus and analysis in the 1820s.
FORMAL DEFINITION OF A LIMIT
Suppose that \(f(x)\) is defined for all \(x\) in an open interval containing \(c\) (but not necessarily at \(x = c\)). Then
\[\lim\limits_{x\rightarrow c}f(x) = L\]
if for all \(\epsilon > 0\), there exists \(\delta > 0\) such that
If the symbols \(\epsilon\) and \(\delta\) seem to make this definition too abstract, keep in mind that we can take \(\epsilon = 10^{-n}\) and \(\delta = 10^{-m}\). Thus, \(\lim\limits_{x\rightarrow c}f(x) = L\) if, for any \(n\), there exist \(m > 0 \) such that \( |f(x) - L| < 10^{-n}\), provided that \(0 < |x - c| < 10^{-m}\).
\[|f(x) - L|<\epsilon \text{ if } 0<|x-c|<\delta\]
The condition \(0 < |x - c| < \delta\) in this definition excludes \(x = c\). In other words, the limit depends only on values of \(f(x)\) near \(c\) but not on \(f(c)\) itself. As we have seen in previous sections, the limit may exist even when \(f(c)\) is not defined.
112
Example 1
Let \(f(x) = 8x + 3\).
(a) Prove that \(\lim\limits_{x\rightarrow 3} f(x) = 27\) using the formal definition of the limit.
(b) Find values of \(\delta\) that work for \(\epsilon = 0.2\) and \(0.001\).
Solution
(a) We break the proof into two steps.
Step 1. Relate the gap to \(|x - c|\).
We must find a relation between two absolute values: \(|f(x) - L|\) for \(L = 27\) and \(|x - c|\) for \(c = 3\). Observe that
\[|f(x)-27|=|(8x+3)-27| = |8x - 24|=8|x-3|\]
Thus, the gap is 8 times as large as \(|x - 3|\).
Step 2. Choose \(\delta\) (in terms of \(\epsilon\)).
We can now see how to make the gap small: If \(|x-3|<\frac{\epsilon}{3}\), then the gap is less than \(8\left(\frac{\epsilon}{8}\right)\). Therefore, for any \(\epsilon > 0\), we choose \(\delta=\frac{\epsilon}{8}\). With this choice, the following statement holds:
\[|f(x) - 27| < \epsilon \text{ if }0< |x-3| < \delta \text{ where } \delta=\frac{\epsilon}{8}\]
Since we have specified \(\delta\) for all \(\epsilon > 0\), we have fulfilled the requirements of the formal definition, thus proving rigorously that \(\lim\limits_{x\rightarrow 3}(8x+3) = 27\).
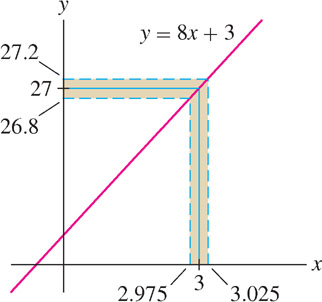
(b) For the particular choice \(\epsilon = 0.2\), we may take \(\delta=\frac{\epsilon}{8} = \frac{0.2}{8} = 0.025\):
\[|f(x) - 27| < 0.2 \text{ if }0< |x-3| < 0.025\]
This statement is illustrated in Figure 2.49. But note that any positive \(\delta\) smaller than \( 0.025 \) will also work. For example, the following statement is also true, although it places an unnecessary restriction on \(x\):
\[|f(x) - 27| < 0.2 \text{ if }0< |x-3| < 0.019\]
Similarly, to make the gap less than \(\epsilon = 0.001\), we may take
\[\delta=\frac{\epsilon}{8} = \frac{0.001}{8} = 0.000125\]
The difficulty in applying the limit definition lies in trying to relate \(|f(x) - L|\) to \(|x - c|\). The next two examples illustrate how this can be done in special cases.
Example 2
Prove that \(\lim\limits_{x\rightarrow 2}x^2 = 4\).
Solution Let \(f(x) = x^2\).
Step 1. Relate the gap to \(|x - c|\).
In this case, we must relate the gap \(|f(x) - 4|\) = \(|x^2 - 4|\) to the quantity \(|x - 2|\) (Figure 2.50). This is more difficult than in the previous example because the gap is not a constant multiple of \(|x - 2|\). To proceed, consider the factorization
\[|x^2 - 4| = |x + 2||x - 2|\]
113
Because we are going to require that \(|x - 2|\) be small, we may as well assume from the outset that \(|x - 2| < 1\), which means that \(1 < x < 3\). In this case, \(|x + 2|\) is less than 5 and the gap satisfies
\[|x^2 - 4| = |x+2||x-2|< 5|x-2|\text{ if }|x-2|< 1 \tag{2}\]
Step 2. Choose \(\delta\) (in terms of \(\epsilon\)).
We see from Eq. (2) that if \(|x - 2|\) is smaller than both \(\frac{\epsilon}{5}\) and 1, then the gap satisfies
\[|x^2 - 4|<5|x-2| <5\left(\frac{\epsilon}{5}\right)=\epsilon\]
Therefore, the following statement holds for all \(\epsilon > 0\):
\[|x^2 - 4|<\epsilon \text{ if }0<|x-2|<\delta \text{ where } \delta\text{ is the smaller of }\frac{\epsilon}{5} \text{ and } 1\]
We have specified \(\delta\) for all \(\epsilon > 0\), so we have fulfilled the requirements of the formal limit definition, thus proving that \(\lim\limits_{x\rightarrow 2}x^2 = 4\).
Example 3
Prove that \(\lim\limits_{x\rightarrow 3}\frac{1}{x} = \frac{1}{3}\).
Solution
Step 1. Relate the gap to \(|x - c|\).
The gap is equal to
\[\left|\frac{1}{x} - \frac{1}{3}\right| = \left|\frac{3-x}{3x}\right| = |x-3|\left|\frac{1}{3x}\right|\]
REMINDER If \(a > b > 0\), then \(\frac{1}{a}<\frac{1}{b}\). Thus, if \(3x > 6\), then \(\frac{1}{3x}<\frac{1}{6}\).
Because we are going to require that \(|x - 3|\) be small, we may as well assume from the outset that \(|x - 3| < 1\) —that is, that \(2 < x < 4\). Now observe that if \(x > 2\), then \(3x > 6\) and \(\frac{1}{3x}<\frac{1}{6}\), so the following inequality is valid if \(|x - 3| < 1\):
\[\left|f(x) - \frac{1}{3}\right| = \left|\frac{3-x}{3x}\right| = |x-3|\left|\frac{1}{3x}\right|<\frac{1}{6}|x-3|\tag{3}\]
Step 2. Choose \(\delta\) (in terms of \(\epsilon\)).
By Eq. (3), if \(|x - 3| < 1\) and \(|x - 3| < 6\epsilon\), then
\[\left|\frac{1}{x} - \frac{1}{3}\right| <\frac{1}{6}|x-3| <\frac{1}{6}(6\epsilon) = \epsilon\]
114
Therefore, given any \(\epsilon > 0\), we let \(\delta\) be the smaller of the numbers \(6\epsilon\) and 1. Then
\[\left|\frac{1}{x} - \frac{1}{3}\right| <\epsilon \text{ if }0<|x-3|<\delta \text{ where } \delta\text{ is the smaller of }6{\epsilon} \text{ and } 1\]
Again, we have fulfilled the requirements of the formal limit definition, thus proving rigorously that \(\lim\limits_{x\rightarrow 3}\frac{1}{x} = \frac{1}{3}\).
GRAPHICAL INSIGHT
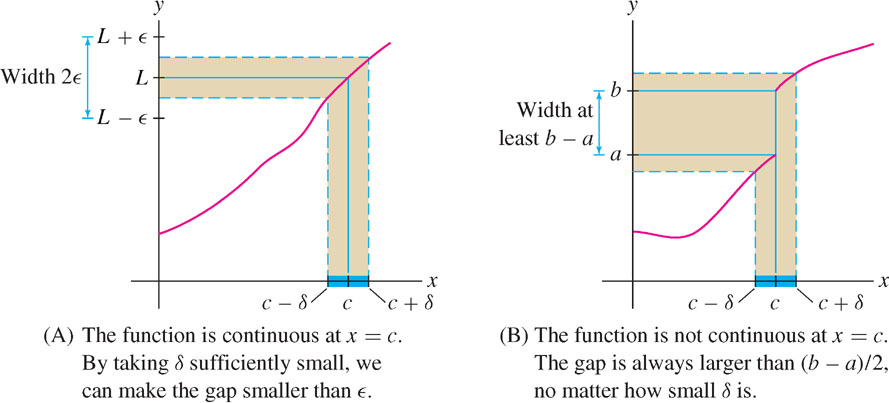
Keep the graphical interpretation of limits in mind. In Figure 2.51(A), \(f(x)\) approaches \(L\) as \(x \rightarrow c\) because for any \(\epsilon > 0\), we can make the gap less than \(\epsilon\) by taking \(\delta\) sufficiently small. By contrast, the function in Figure 2.51(B) has a jump discontinuity at \(x = c\). The gap cannot be made small, no matter how small \(\delta\) is taken. Therefore, the limit does not exist.
2.9.2 Proving Limit Theorems
In practice, the formal limit definition is rarely used to evaluate limits. Most limits are evaluated using the Basic Limit Laws or other techniques such as the Squeeze Theorem. However, the formal definition allows us to prove these laws in a rigorous fashion and thereby ensure that calculus is built on a solid foundation. We illustrate by proving the Sum Law and another useful result. Other proofs are given in Appendix D.
Proof of the Sum Law
Assume that
\[\lim\limits_{x\rightarrow c}f(x) = L \text{ and }\lim\limits_{x\rightarrow c}g(x) = M\]
We must prove that \(\lim\limits_{x\rightarrow c}(f(x)+g(x)) = L+M\).
REMINDER The Triangle Inequality [Eq. (1) in Section 2.5] states
\[|a + b| \leq |a|+|b|\]
for all \(a\) and \(b\).
Apply the Triangle Inequality (see margin) with \(a = f(x)- L\) and \(b = g(x) - M\):
\[|f(x)+g(x) - (L+M)|\leq |f(x) - L| + |g(x) - M|\tag{4}\]
Each term on the right in (4) can be made small by the limit definition. More precisely, given \(\epsilon > 0\), we can choose \(\delta\) such that \(|f(x) - L|<\frac{\epsilon}{2}\) and \(|g(x) - M|<\frac{\epsilon}{2}\) if \(0 < |x-c| < \delta\) (in principle, we might choose different \(\delta\)’s for \(f\) and \(g\), but we may then use the smaller of the two \(\delta\)’s). Thus, Eq. (4) gives
\[|f(x)+g(x) - (L+M)|<\frac{\epsilon}{2} + \frac{\epsilon}{2} = \epsilon \text{ if }0<|x-c|<\delta\tag{5}\]
115
This proves that
\[\lim\limits_{x\rightarrow c}(f(x)+g(x)) = L+M = \lim\limits_{x\rightarrow c}f(x) + \lim\limits_{x\rightarrow c}g(x)\]
Another example to apply our formal definition of limit is to Theorem 1 from Section 2.2. We stated that the limit itself exists if and only if both one-sided limits exist and are equal. We are now able to formally prove this, and the proof is straightforward.
For a video of a proof of this theorem, click here.
2.9.3 Section 2.9 Summary
- Informally speaking, the statement \(\lim\limits_{x\rightarrow c}f(x) = L\) means that the gap \(|f(x) - L|\) tends to \(0\) as \(x\) approaches \(c\).
- The formal definition (called the \(\epsilon-\delta\) definition): \(\lim\limits_{x\rightarrow c}f(x) = L\) if, for all \(\epsilon > 0\), there exists a \(\delta > 0\) such that
\[|f(x) - L|< \epsilon\text{ if }0<|x-c|<\delta\]